Menentukan posisi bulan termasuk hal penting dalam ilmu hisab. Misalnya, menentukan berapakah azimuth dan ketinggian bulan pada saat maghrib pada hari terjadinya ijtimak atau hari sesudahnya. Juga, menentukan kapan bulan terbit, transit dan terbenam jika diamati dari suatu tempat tertentu.
Pada tulisan sebelumnya, telah dijabarkan bagaimanakah cara menentukan posisi matahari. Pada kesempatan ini, penulis akan menjelaskan cara menghitung posisi bulan di langit berdasarkan teori Brown. Ernest W. Brown adalah seorang astronom berkebangsaan Inggris abad 19. Seperti biasa, pertama kali akan dihitung posisi bulan menurut koordinat ekliptika geosentrik, yaitu nilai bujur ekliptika (lambda), lintang ekliptika (beta) dan jarak bumi-bulan.
Selanjutnya, dengan menggunakan epsilon (sudut antara bidang ekliptika dengan bidang ekuator, sekitar 23,5 derajat), lambda, beta serta trannsformasi koordinat antara koordinat ekliptika geosentrik dengan ekuator geosentrik, maka posisi bulan menurut koordinat ekuator geosentrik dapat dihitung. Dalam hal ini, right ascension (alpha) dan deklinasi (delta). Nilai alpha dapat diubah menjadi hour angle (HA) dengan memanfaatkan Local Sidereal Time dan bujur geografis tempat pengamatan. Akhirnya, dengan menggunakan transformasi dari koordinat ekuator geosentrik ke horison, maka sudut azimuth dan altitude bulan dapat ditentukan.
Jika bulan diproyeksikan/ditarik tegaklurus ke bidang horison/ufuk, maka altitude adalah sudut ketinggian bulan dari ufuk, sedangkan azimuth, seperti telah dijelaskan pada tulisan-tulisan sebelumnya adalah sudut antara titik utara (azimuth 0 derajat) dengan titik proyeksi bulan di ufuk yang diukur dari arah utara mengikuti arah jarum jam.
Metode menentukan posisi bulan menurut algoritma Brown adalah sebagai berikut. Dari tanggal dan waktu, konversikan waktunya menjadi UT. Dari UT, ubahlah menjadi TD dengan menambahkan Delta_T. Selanjutnya tentukan nilai Julian Day Ephemeris (JDE) untuk waktu TD tersebut.
- T = (JDE – 2451545)/36525.
- Bujur rata-rata bulan = U = 218,317 + 481267,883*T.
- Anomali rata-rata bulan = V = 134,954 + 477198,849*T.
- Bujur rata-rata titik naik bulan = Omega = 125,041 – 1934.142*T.
- Bujur rata-rata matahari = L = 280,466 + 36000,769*T.
- Anomali rata-rata matahari = M = 357,526 + 35999.050*T.
- Satuan U, V, Omega, L dan M adalah derajat dengan rentang nilai antara 0 hingga 360 derajat. Jika nilainya diluar rentang itu, kurangkan atau tambahkan dengan kelipatan 360 derajat.
Bujur Ekliptika Bulan
Untuk menentukan bujur ekliptika bulan yang sebenarnya, perlu dihitung koreksi bujur bulan yang berjumlah enam buah. Enam buah faktor koreksi itu berkaitan dengan
- – bentuk orbit bulan. Koreksi1 = 22640*SIN(V) + 769*SIN(2*V) + 36*SIN(3*V).
- – ketidaksamaan paralaks. Koreksi2 = -125*SIN(U – L).
- – variasi. Koreksi 3 = 2370*SIN(2*(U – V)).
- – persamaan tahunan. Koreksi4 = -668*SIN(M).
- – kemiringan orbit bulan. Koreksi5 = -412*SIN(2*(U – Omega)) + 212*SIN(2*(U – L – V)).
- – eveksi. Rumusnya agak panjang. Koreksi6 = 4586*SIN(2*(U – L) – V) + 206*SIN(2*(U – L) – V – M) + 192*SIN(2*(U – L) + V) + 165*SIN(2*(U – L) – M) + 148*SIN(V – M) – 110*SIN(V + M).
- Total koreksi adalah jumlah keenam koreksi di atas. Faktor koreksi di atas bersatuan detik busur. Jadi harus dibagi 3600 agar bersatuan derajat.
Akhirnya bujur bulan sesungguhnya (Lambda) menurut teori Brown adalah Lambda = Bujur rata-rata bulan (U) + Total Koreksi.
Lintang Ekliptika Bulan
- Lintang Ekliptika Bulan (Beta) dapat dihitung dengan rumus sebagai berikut
- Beta = 18520*SIN(Lambda – Omega + 0,114*SIN(2*(U – Omega)) + 0,150*SIN(M)) – 526*SIN(2*L – U – Omega) + 44*SIN(2*L – U – Omega + V) – 31*SIN((2*L – U – Omega – V) – 23*SIN((2*L – U – Omega + M) + 11*SIN((2*L – U – Omega – M) – 25*SIN(U – Omega – 2*V) + 21*SIN(U – Omega – V).
- Beta menurut rumus di atas bersatuan detik busur. Jadi harus dibagi 3600 agar bersatuan derajat.
Jarak Bumi-Bulan
- Untuk menentukan jarak bumi-bulan, terlebih dahulu dihitung sudut paralaks bumi-bulan = Phi = 3423 + 187*COS(V) + 10*COS(2*V) + 34*COS(2*(U – L) – V) + 28*COS(2*(U – L)) + 3*COS(2*(U – L) + V).
- Phi bersatuan detik busur. Jadi harus dibagi 3600 agar bersatuan derajat.
- Sudut jari-jari bulan (s) dapat dihitung dengan rumus
- SIN(s) = 0,272493*SIN(Phi).
- s = ASIN(0,272493*SIN(Phi)).
- Jarak Bumi-Bulan = R = 6378,14/SIN(Phi).
- Satuan s adalah derajat.Satuan R adalah km.
Jika Bujur Ekliptika Bulan (Lambda) dan Lintang Ekliptika Bulan (Beta) sudah diketahui, maka selanjutnya dapat dicari Right Ascension Bulan (Alpha) dan Deklinasi Bulan (Delta). Disini tentu perlu dihitung dahulu nilai Epsilon, yaitu sudut antara bidang ekliptika dengan bidang ekuator. Penulis sudah pernah jelaskan masalah ini pada tulisan sebelumnya. Alpha dan Delta dapat dicari dengan menggunakan transformasi koordinat dari ekliptika geosentrik ke ekuator geosentrik. Silakan baca tulisan tentang TRANSFORMASI SISTEM KOORDINAT.
Dari nilai Alpha dan Delta tersebut, Azimuth dan Altitude Bulan pada waktu tertentu yang diamati di tempat tertentu (Bujur dan Lintang Geografis) juga dapat diketahui. Seperti telah dijelaskan pada tulisan TRANSFORMASI SISTEM KOORDINAT, terlebih dahulu dicari nilai Hour Angle (HA) yang dihitung dari Local Sidereal Time (LST), bujur geografis dan zona waktu lokal tempat tersebut. Dari Hour Angle, Delta dan lintang geografis yang telah diketahui, akhirnya azimuth dan altitude bulan dapat ditentukan.
Contoh
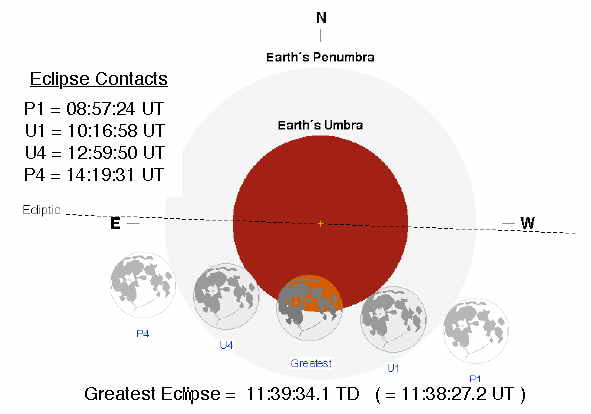
Pada tanggal 22 Juli 2009, Insya Allah akan terjadi gerhana matahari total. Menurut algoritma Meeus, gerhana maksimum akan terjadi pada pukul 02:36:36 TD atau pukul 02:35:29,5 UT (Delta T = 66,5 detik). Tentukan posisi bulan pada waktu tersebut, diukur dari koordinat 24,2 derajat N dan 144,1 derajat E (tempat teramatinya gerhana matahari total maksimum tersebut). Zona waktu tempat tersebut = UT + 9.
Jawab
- Tanggal 22 Juli 2009 pukul 02:36:36 TD bersesuaian dengan JDE = 2455034,60875.
- Karena itu nilai T = 0,09554028063.
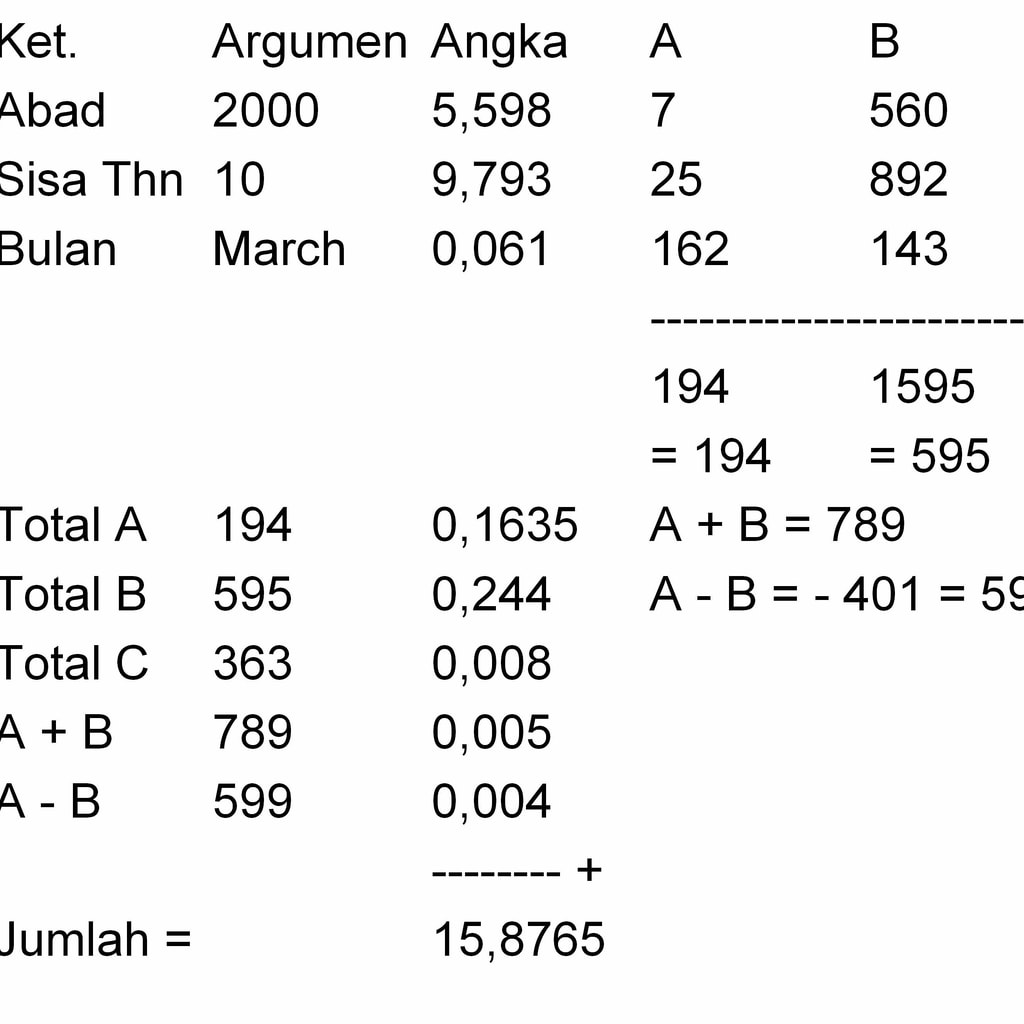
- Selanjutnya dapat dihitung lima sudut argumen sebagai berikut.
- Bujur rata-rata bulan = 118,7856 derajat.
- Anomali rata-rata bulan = 6,66595 derajat.
- Omega = 300,25253 derajat.
- Bujur rata-rata matahari = 119,98957 derajat.
- Anomali rata-rata matahari = 196,88534 derajat.
- Untuk menentukan bujur ekliptika bulan, dapat dihitung enam buah koreksi, dimana total koreksi = 2384,260675 detik busur = 0,66229 derajat.
- Akhirnya Bujur ekliptika bulan = 119,44789 derajat = 119:26:52 derajat (119 derajat 26 menit busur 52 detik busur).
- Sementara itu lintang ekliptika bulan atau beta dapat dihitung = 0,068860 derajat = 0:4:8 derajat.
- Sudut paralaks bulan = 1:01:23 derajat, sehingga sudut jari-jari bulan = 0:16:44 derajat.
- Jarak bumi-bulan dapat dihitung = 357215 km.
- Nilai epsilon dapat dihitung = 23,439257 derajat.
- Dengan menggunakan transformasi koordinat dari ekliptika ke ekuator geosentrik, diperoleh
- Right ascension bulan (alpha) adalah pukul 8:6:29.
- Deklinasi bulan (delta) = 20:20:1 derajat.
- Selanjutnya digunakan transformasi koordinat dari ekuator geosentrik ke horison.
- Diamati dari posisi 24,2 derajat N dan 144,1 derajat E, azimuth dan altitude bulan pada waktu tersebut berturut-turut adalah 198:1:47 derajat dan 85:56:24 derajat.
Adapun, posisi matahari diukur dari tempat yang sama pada waktu yang sama adalah azimuth matahari 197:57:24 derajat dan altitude matahari 85:52:20 derajat. Silakan pembaca menghitung sendiri posisi matahari dengan cara yang telah diberikan pada tulisan sebelumnya tentang MENENTUKAN POSISI MATAHARI, atau dengan menggunakan file MS Excel yang penulis lampirkan dalam tulisan tersebut.
Nampak bahwa selisih azimuth bulan dan matahari adalah sekitar 4 menit busur (1 derajat = 60 menit busur). Adapun selisih altitude bulan dan matahari adalah sekitar 4 menit busur. Dengan menggunakan rumus separasi sudut, sudut jarak antara bulan-matahari adalah sekitar 4 menit busur pula. Angka ini jauh lebih kecil daripada sudut jari-jari bulan maupun matahari yang besarnya sekitar 16 menit busur. Jadi bulan dan matahari nampak berimpit sehingga memang terjadi gerhana matahari. Gerhana ini memang dapat diamati dari tempat tersebut, karena altitudenya positif dan waktu saat itu adalah di siang hari (pukul 11:35 waktu setempat).
Pembahasan lebih lengkap mengenai gerhana matahari total 22 Juli 2009 Insya Allah diberikan pada tulisan mendatang.
Dari perhitungan di atas, posisi bulan dapat disimpulkan sebagai berikut.
- Bujur ekliptika bulan = 119:26:52 derajat.
- Lintang ekliptika bulan = 0:4:8 derajat.
- Sudut jari-jari bulan = 0:16:44 derajat
- Jarak bumi-bulan = 357215 km.
- Right Ascension bulan = pukul 8:6:29.
- Deklinasi bulan = 20:20:1 derajat.
- Jika diukur dari tempat tersebut, azimuth bulan = 198:1:47 derajat dan altitude bulan = 85:56:24 derajat.
Sebagai perbandingan, algoritma ELP2000 yang terakurat dalam menentukan posisi bulan memberikan hasil sebagai berikut.
- Bujur ekliptika bulan = 119:27:5 derajat.
- Lintang ekliptika bulan = 0:4:14 derajat.
- Sudut jari-jari bulan = 0:16:43 derajat.
- Jarak bumi-bulan = 357531 km..
- Right Ascension bulan = pukul 8:6:30.
- Deklinasi bulan = 20:20:5 derajat.
- Jika diukur dari tempat tersebut, azimuth bulan = 198:0:32 derajat dan altitude bulan = 85:56:30 derajat.
Nampak disini algoritma Brown sudah sangat memadai untuk menentukan posisi bulan. Selisih hasilnya dengan algoritma ELP2000 hanya berkisar beberapa detik busur saja. Adapun selisih jarak bumi-bulan antara kedua algoritma hanya sekitar 300 km, yang jauh lebih kecil daripada jari-jari bulan (sekitar 1731 km) itu sendiri. Adapun pembahasan tentang algoritma ELP2000 yang disebut paling akurat dalam menentukan posisi bulan, Insya Allah diberikan pada kesempatan lain.
Rumus-rumus posisi bulan di atas berdasarkan algoritma Brown sudah penulis susun dalam file MS Excel yang dapat didownload di.
http://www.4shared.com/file/116396119/a30e2d26/Posisi-Bulan.html
Semoga bermanfaat.
DR. RINTO ANUGRAHA
Saat ini sebagai peneliti pasca doktoral dalam bidang Nonlinear Physics di Kyushu University, Fukuoka, JAPAN.
Referensi:
- Oliver Montenbruck, Practical Ephemeris Calculation, Springer-Verlag, Berlin, 1989.
- Jean Meeus: Astronomical Algorithm, Willmann-Bell, Virginia, 1991.
- Mohamad Odeh, Accurate Times v.5.1.
- NASA, Five Millennium Catalog of Solar Eclipses.